COLEGIO DE BACHILLERES DEL ESTADO DE OAXACA
PLANTEL 04 "EL TULE"
ACTIVIDADES DE PAGINAS 48,49,50, CONSTRUYE T Y MAS
MATEMATICAS
NOMBRE: Pedro Matthew Díaz Aquino
PROFESOR: Alejandro Enrique Vasquez Martinez
CICLO ESCOLAR : 2020 "A"
RESÚMENES
Formas de medir un angulo
Radianes: Un radián es la unidad de medida de un ángulo con vértice en el centro de una circunferencia y cuyos lados delimitan un arco de circunferencia que tiene la misma longitud que el radio. El radián (rad) es la unidad de medida para ángulos en el Sistema Internacional de Unidades (S.I.)
La relación del radián con la otra unidad de medida para ángulos más ampliamente utilizada, los grados sexagesimales o simplemente grados (º), es la siguiente:
1 vuelta completa de la circunferencia = 360º = 2 · π radianes
Para entender la anterior igualdad, se parte de saber que la medida en radianes de un ángulo (θ) medido en una circunferencia es igual a la longitud del arco que abarca dividida entre el radio de dicha circunferencia, es decir:θ(radianes) = Longitud del arco / Radio
Por tanto, cuando se trata del ángulo correspondiente a una circunferencia completa, cuya longitud total es 2·π·r (siendo r el radio de la circunferencia) le corresponden en radianes un ángulo de:
θ(circunferencia completa) = 2·π·r / r = 2·π radianes
En el sistema sexagesimal, el ángulo que abarca la circunferencia completa mide 360º, por lo que se puede establecer la ya vista relación entre grados y radianes:
1 vuelta completa = 360º = 2 · π radianes
Otras equivalencias útiles entre grados y radianes son las siguientes:
0º = 0 rad
90º = π/2 rad
180º = π rad
Sistema sexagesimal: El sistema sexagesimal es un sistema de unidades muy empleado cuyo fundamento es que cada unidad se divide en 60 unidades de una orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad fundamentalmente para la medida de ángulos y también en la medida del tiempo. La unidad de medida de ángulos en el sistema sexagesimal es el grado (º), que es el resultado de dividir el ángulo llano en 180 partes iguales, o bien un ángulo recto en 90 partes, o un ángulo completo en 360 partes. A cada una de esas partes se les llama grado (º). Así, un ángulo llano mide 180º, un ángulo recto 90º y un ángulo completo 360º.
A su vez, cada grado se subdivide en otras unidades inferiores, en concreto, en sesenta partes iguales. De esta manera, cada grado se divide en 60 minutos (1º = 60´) y cada minuto, a su vez, en 60 segundos (1´ = 60´´).
Sistema centesimal: El sistema centesimal divide una circunferencia en 400 partes iguales, o bien, un ángulo recto en 100 partes iguales, y a cada una de esas partes se le denomina grado centesimal o gradián, y se simboliza con una «g» minúscula como superíndice del número, por ejemplo 35g
A su vez, cada grado centesimal se subdivide en unidades más pequeñas dividiéndolo en cien partes iguales, y dando lugar al minuto. Así, el minuto (m) en este sistema es la centésima parte del grado (1g = 100m) y el segundo (s) la centésima parte del minuto (1m = 100s).
De la misma manera, el segundo se divide en décimas, centésimas, milésimas,... Un ejemplo de un ángulo expresado según el sistema centesimal sería: 40g 30m 10s.
Por otro lado, el método para expresar en forma decimal un grado expresado en minutos y segundos centesimales es muy sencillo, ya que basta con colocar una coma después de los grados, así 40g 30m 10s = 40,3010g.
Y la conversión inversa, es decir, para pasar de grados centesimales en forma decimal a minutos y segundos centesimales se realiza como se indica en el siguiente ejemplo:
- Pasar 26,2547g a grados minutos y segundos centesimales
26,2547g = 26g + 0,25 · 100 + 0,0047 · 10000 = 26g + 25m + 47s
RESÚMENES
Formas de medir un anguloRadianes: Un radián es la unidad de medida de un ángulo con vértice en el centro de una circunferencia y cuyos lados delimitan un arco de circunferencia que tiene la misma longitud que el radio. El radián (rad) es la unidad de medida para ángulos en el Sistema Internacional de Unidades (S.I.)
La relación del radián con la otra unidad de medida para ángulos más ampliamente utilizada, los grados sexagesimales o simplemente grados (º), es la siguiente:
1 vuelta completa de la circunferencia = 360º = 2 · π radianes
Para entender la anterior igualdad, se parte de saber que la medida en radianes de un ángulo (θ) medido en una circunferencia es igual a la longitud del arco que abarca dividida entre el radio de dicha circunferencia, es decir:θ(radianes) = Longitud del arco / Radio
Por tanto, cuando se trata del ángulo correspondiente a una circunferencia completa, cuya longitud total es 2·π·r (siendo r el radio de la circunferencia) le corresponden en radianes un ángulo de:
θ(circunferencia completa) = 2·π·r / r = 2·π radianes
En el sistema sexagesimal, el ángulo que abarca la circunferencia completa mide 360º, por lo que se puede establecer la ya vista relación entre grados y radianes:
1 vuelta completa = 360º = 2 · π radianes
Otras equivalencias útiles entre grados y radianes son las siguientes:
0º = 0 rad
90º = π/2 rad
180º = π rad
Sistema sexagesimal: El sistema sexagesimal es un sistema de unidades muy empleado cuyo fundamento es que cada unidad se divide en 60 unidades de una orden inferior, es decir, es un sistema de numeración en base 60. Se aplica en la actualidad fundamentalmente para la medida de ángulos y también en la medida del tiempo. La unidad de medida de ángulos en el sistema sexagesimal es el grado (º), que es el resultado de dividir el ángulo llano en 180 partes iguales, o bien un ángulo recto en 90 partes, o un ángulo completo en 360 partes. A cada una de esas partes se les llama grado (º). Así, un ángulo llano mide 180º, un ángulo recto 90º y un ángulo completo 360º.
A su vez, cada grado se subdivide en otras unidades inferiores, en concreto, en sesenta partes iguales. De esta manera, cada grado se divide en 60 minutos (1º = 60´) y cada minuto, a su vez, en 60 segundos (1´ = 60´´).
Sistema centesimal: El sistema centesimal divide una circunferencia en 400 partes iguales, o bien, un ángulo recto en 100 partes iguales, y a cada una de esas partes se le denomina grado centesimal o gradián, y se simboliza con una «g» minúscula como superíndice del número, por ejemplo 35g
Milésima artillera:La milésima artillera o MIL ANGULAR es una unidad de medida de ángulos utilizada en el ámbito militar, principalmente en instrumentos de orientación y señalización.La milésima artillera surge de la necesidad de aumentar la precisión en el uso de armamento cada vez más avanzado, y donde el uso de medidas angulares, como los grados sexagesimales o centesimales, no podían responder a esta necesidad debido a que son unidades de medidas demasiado grandes para las cada vez más modernas y potentes piezas de artillería. Por tanto, era necesaria una nueva y más precisa unidad de medida para los aparatos que proporcionaban los ángulos de alcance y deriva de los modernos cañones y demás armas. Nacía así la milésima artillera.
La nueva medida angular resultaba de dividir en 6400 partes iguales una circunferencia, en comparación de las sólo 360 divisiones de los grados sexagesimales o las 400 de los centesimales, y a cada una de estas partes se la denomina milésima artillera.
Por tanto, haciendo uso de la milésima artillera, un ángulo recto de 90º podía dividirse en 1600 partes iguales, por lo que se podía determinar más exactamente la posición de cualquier objetivo.
La milésima artillera, al igual que los grados sexagesimales o centesimales, es una medida angular que se puede definir también como el ángulo con el que vemos una varilla de un metro de alta a 1 Km. de distancia.
Para pasar de radianes a grados sexagesimales hay que recordar la relación para un ángulo que describe una circunferencia completa expresado en grados y radianes, como:
360º = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresadas en grados y radianes es la siguiente
La nueva medida angular resultaba de dividir en 6400 partes iguales una circunferencia, en comparación de las sólo 360 divisiones de los grados sexagesimales o las 400 de los centesimales, y a cada una de estas partes se la denomina milésima artillera.
Por tanto, haciendo uso de la milésima artillera, un ángulo recto de 90º podía dividirse en 1600 partes iguales, por lo que se podía determinar más exactamente la posición de cualquier objetivo.
La milésima artillera, al igual que los grados sexagesimales o centesimales, es una medida angular que se puede definir también como el ángulo con el que vemos una varilla de un metro de alta a 1 Km. de distancia.
MÉTODOS DE CONVERSIÓN ENTRE SISTEMAS DE MEDIDA DE ÁNGULOS
Pasar de radianes a grados sexagesimales
Pasar de radianes a grados sexagesimales
Para pasar de radianes a grados sexagesimales hay que recordar la relación para un ángulo que describe una circunferencia completa expresado en grados y radianes, como:
360º = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresadas en grados y radianes es la siguiente
| G | = | R |
| 360º | 2 · π |
donde,
G es la medida del ángulo expresada en grados sexagesimales (º)
R es la medida del ángulo expresada en radianes (rad)
Si lo que se desea es calcular los grados sexagesimales a partir de radianes, se despeja G de la expresión anterior, quedando:
R
| ||
G =
|
· 360º
| |
2·π
|
Pasar de radianes a grados centesismos: Para pasar de radianes a grados centesimales se parte de la relación que hay para un ángulo que describe una circunferencia completa expresado en grados centesimales y radianes:
400 g = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresadas en grados centesimales y radianes es la siguiente:
| C | = | R |
| 400g | 2 · π |
donde,
C es la medida del ángulo expresada en grados centesimales (g)
R es la medida del ángulo expresada en radianes (rad)
Si lo que se pide es calcular los grados centesimales a partir de radianes, se despeja C de la expresión anterior, quedando:
R
| ||
C =
|
· 400 g
| |
2·π
|
Pasar de grados sexagesimales a radianes:
Para pasar de grados sexagesimales a radianes se parte de nuevo de la relación de un ángulo completo expresado en grados sexagesimales y radianes:
360º = 2 · π radianes
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresado en grados sexagesimales y radianes es la ya conocida:
| G | = | R |
| 360º | 2 · π |
donde,
G es la medida del ángulo expresada en grados sexagesimales (º)
R es la medida del ángulo expresada en radianes (rad)
Si lo que se desea es calcular el valor en radianes de un ángulo expresado en grados sexagesimales, se despeja R de la expresión anterior, quedando:
G
| ||
R =
|
· 2 · π
| |
360º
|
Pasar de grados sexagesimales a grados centesimales
Para pasar de grados sexagesimales a centesimales se parte de la relación del ángulo que describe una circunferencia completa expresado en grados sexagesimales y centesimales:
1 vuelta completa = 360º = 400 g
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresado en grados sexagesimales y centesimales sería:
| G | = | C |
| 360º | 400 g |
donde,
G es la medida del ángulo expresada en grados sexagesimales (º)
C es la medida del ángulo expresada en grados centesimales (g)
Si lo que se pide es calcular los grados centesimales a partir de grados sexagesimales, se despeja C de la expresión anterior, quedando:
G
| ||
C =
|
· 400 g
| |
360º
|
Pasar de grados centesimales a grados sexagesimales
Para pasar de grados centesimales a sexagesimales se parte, como en el apartado anterior, de la relación del ángulo que describe una circunferencia completa expresado en grados centesimales y sexagesimales:
1 vuelta completa = 400 g = 360º
Por tanto, de nuevo la expresión general que permite relacionar las medidas de un ángulo expresado en grados centesimales y sexagesimales sería:
| C | = | G |
| 400 g | 360º |
donde,
C es la medida del ángulo expresada en grados centesimales (g)
G es la medida del ángulo expresada en grados sexagesimales (º)
Si lo que se pide es calcular los grados sexagesimales a partir del ángulo expresado en grados centesimales, se despeja G de la expresión anterior, quedando:
C
| ||
G =
|
· 360º
| |
400 g
|
Pasar milésimas artilleras a grados sexagesimales
La milésima artillera o mil angular es un sistema de medida de ángulos que resultaba de dividir en 6400 partes iguales una circunferencia completa. Por tanto, la relación entre milésimas artilleras y grados sexagesimales es la siguiente:
1 vuelta completa = 6400ºº = 360º
La relación anterior también se puede expresar en función del ángulo recto. En este caso, la milésima artillera es la que resulta de dividir un ángulo recto (90º en el sistema sexagesimal) en 1600 partes iguales, es decir, que:
¼ de vuelta = 1600ºº = 90º
| MIL | = | G |
| 1600ºº | 90º |
donde,
MIL es la medida del ángulo expresada en milésimas artilleras (ºº)
G es la medida del ángulo expresada en grados sexagesimales (º)
Si lo que se pide es calcular los grados sexagesimales a partir del ángulo expresado en milésimas artilleras, se despeja G de la expresión anterior, quedando:
MIL
| ||
G =
|
· 90º
| |
1600ºº
|
Pasar milésimas artilleras a grados centesimales
Como se ha dicho en el apartado anterior, la milésima artillera es la medida angular que resultaba de dividir en 6400 partes iguales una circunferencia completa, mientras que en grados centesimales una circunferencia completa son 400g, por tanto:
1 vuelta completa = 6400ºº = 400 g
Si se prefiere, la relación anterior también se puede expresar en función del ángulo recto. En este caso, la milésima artillera es la que resulta de dividir un ángulo recto (100g en el sistema centesimal) en 1600 partes iguales, es decir, que:
¼ de vuelta = 1600ºº = 100 g
Por tanto, la expresión general que permite relacionar las medidas de un ángulo expresado en milésimas artilleras y grados centesimales es la siguiente:
| MIL | = | C |
| 1600ºº | 100g |
donde,
MIL es la medida del ángulo expresada en milésimas artilleras (ºº)
C es la medida del ángulo expresada en grados centesimales (g)
Si lo que se pide es calcular los grados centesimales a partir del ángulo expresado en milésimas artilleras, se despeja C de la expresión anterior, quedando:
MIL
| ||
C =
|
· 100g
| |
1600ºº
|
RAZONES TRIGONOMÉTRICAS
Seno
El seno del ángulo B es la razón entre el cateto opuesto al ángulo y la hipotenusa. Se denota por sen B.
Coseno
El coseno del ángulo B es la razón entre el cateto adyacente o contiguo al ángulo y la hipotenusa. Se denota por cos B.
Tangente
La tangente del ángulo B es la razón entre el cateto opuesto al ángulo y el cateto adyacente al ángulo. Se denota por tan B o tg B.
Cosecante
La cosecante del ángulo B es la razón inversa del seno de B.
Se denota por csc B o cosec B.
Secante
La secante del ángulo B es la razón inversa del coseno de B.
Se denota por sec B.
Cotangente
La cotangente del ángulo B es la razón inversa de la tangente de B.
Se denota por cot B o ctg B.
ÁNGULOS DE ELEVACIÓN Y DEPRESIÓN
Angulo de elevación: El ángulo de elevación (usado indistintamente como ángulo de altitud) es la altura angular del sol en el cielo medido desde la horizontal. Este ángulo máximo de elevación se produce al mediodía solar y depende del ángulo de latitud y declinación.
Angulo de depresión: El término ángulo de depresión denota al ángulo desde la horizontal hacia abajo a un objeto. Una línea de vista para el observador estaría debajo de la horizontal.
ASPECTOS COMUNES DE ÁNGULOS DE ELEVACIÓN Y DEPRESIÓN
SE PODRÍA DECIR QUE:
-Son un el mismo angulo pero cabido de posición o son una representación opuesta de el otro
-Son una vista de el sol, el angulo que da
CARACTERÍSTICAS PARA LA MEDICIÓN DE LOS ÁNGULOS EN TRIGONOMÉTRICA
Los ángulos se miden en grados y en radianes. En el sistema sexagesimal la unidad de medida es el grado ° y en el sistema cíclico la unidad de medida de los ángulos es el radián.
El Grado: Se define como 1/360 de la rotación total.
l Radián: Se define como la medida de un ángulo central de una circunferencia cuyo arco mide igual que un radio.
En toda circunferencia hay aproximadamente 6.28 radianes, es decir, 2π radianes.
2.6 QUITARNOS LAS ETIQUETAS QUE NO NOS AYUDAD
b.¿Qué le dirían a Naty para ayudarla con base en la reflexión de los incisos anteriores ? "oye ¿estas bien?" "así pasa, ya veras que luego todo pasara"
c. ¿Cómo podría sentirse mejor?Expliquen su respuesta?
Pues sencillamente apoyándola , haciéndola sentir que tiene apoyo de alguien
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA LECCIÓN
Que aunque haya malos momentos, pasaran, por que después de la tormenta llega la calma , todo pasara y mejoraras como persona
4.6 EL BOTÓN DE LA ANSIEDAD ACADÉMICA
Actividad 1
a. De manera individual , lee los siguientes comentarios:
NIÑA:¿Que situación me causa malestar? pues ,definitivamente hacer los ejercicios de matemáticas yo sola, me siento mal cuando no me salen a la primera
NIÑO: a mi me pasa cuando tengo que hablar en la clase de ingles , tiemblo mucho , se me olvidan las palabras
NIÑO: siento lo mismo cuando paso al lado del grupito que va en el ultimo año , me dan miedo y siento que me podrían molestar
b. Describe una situación que te cause malestar,nerviosismo, rechazo, etcétera . Escribe que pensabas en ese momento y qué sentías en tu cuerpo.:pues una vez que tenia que hacer una mascara de un personaje, no sabia como rayos iba a hacer una mascara, ni como decorarla, estaba super confundido
c. La situación del inciso anterior probablemente sea de ansiedad académica . revisa la definición del concepto clave y responde¿Qué implicación ha tenido la ansiedad académica en tu vida escolar? pues gracias a ella tengo mucho o tenia mucho nerviosismo ante cualquier tarea importante, grande o larga
¿Qué consecuencias te podría traer a futuro? darme miedo al querer una carrera muy difícil y exigente que me guste
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA REACCIÓN
Qué aunque sea mala la ansiedad académica, se puede vencer si te esfuerzas en ello
5.6 TRABAJAR EL BOTÓN DE LA ANSIEDAD
Actividad 1. Trabajen en completando el ultimo cuadro de la historia que te presentamos a continuación
Primer examen de matemáticas: deje el estudio para el ultimo momento, no me dio tiempo de cubrir todos los temas y me acosté tarde. Dormí mal. No alcance a desayunar, llegue corriendo , tarde y con agitación. Sentía incomodidad y mis músculos estaban tensos, me empece a sentir mal, no podia concentrarme en el examen.Este conflicto interno entre quererme sentir mejor y tener que aprobar el examen fue muy desagradable. Así paso 2 veces .
MARIANA MARTINEZ
MI BOTÓN: Presentar exámenes de matemáticas
EMOCIÓN QUE ME GENERA:Ansiedad
ESTRATEGIA PARA CAMBIAR ESE BOTÓN (MUNDO O SITUACIÓN): Para el próximo examen de matemáticas voy a estudiar con tiempo y poco a poco
TERCER EXAMEN: Estudie con tiempo, cubrí estudiar todos los temas y me acosté temprano para el examen, dormí bien, desayune tranquilo, llegue tranquilo al salón, con tiempo, estaba relajada, me sense y me sentí normal, empece a concentrarme en el examen y al final me fue de maravilla
Actividad 2 en la variación 4.6 que escribiste de una situación recurrente ("botón")
a. Anótala nuevamente : una vez que tenia que hacer una mascara de un personaje , no sabia como rayos iba a hacer una mascara ni como decorarla, estaba confundido
b. piensa y anota cómo podrías aplicar la "estrategia de cambiar al mundo para disminuir su intensidad": pensar con la mente tranquila y fría , pensando rápido que usare para decorar esa mascara y sobretodo como hacerla
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA LECCIÓN: que siempre si quiere estar tranquilo sin preocupaciones , has lo que tengas que hacer con tiempo
6.6 CUANDO LLEGA EL HURACAN
a. Lean el siguiente texto
Alejandria y Paconio eran dos pueblos vecinos a los que se les aviso de la venida de un huracan, Alejandria se preparo, reforzo sus casas, guardaron agua, comida , linternas y velas, mientras paconio dijo que no habia problema con el huracan que seria suave.El huracan llego, fue muy fuerte y dejo sin luz ni agua en varios dias, muchas casas se levantaron.
a. Ahora imaginemos a dos estudiantes: maria y omar , ambos les llega el botón del enojo cuando deben hacer equipos de matemáticas, maria se calma y se prepara pero omar ocupa la estrategia de paconio
b. completen la siguiente
1.¿Qué hace antes de que llegue el enojo? 2.¿Qué hace, piensa durante el enojo? 3.¿qué hace después?
Secuencias para representar y calcular ángulos de referencia
Ángulo de referencia
Digamos que θ es un ángulo de ningún cuadrante en posición estándar. Su ángulo de referencia es el ángulo agudo a formado por el lado terminal de θ y el eje horizontal.
Cuadrante I: El ángulo dado y el ángulo de referencia son el mismo ángulo.
α = θ

Cuadrante II: α = π – θ (radianes)
α = 180°– θ (grados)

Cuadrante III: α = θ – π (radianes)
α = θ – 180° (grados)

Cuadrante IV: α = 2 π – θ (radianes)
α = 360° – θ (grados)

Circulo unitario y funciones trigonométricas
Las funciones trigonométricas, parece haber tenido su origen en las investigaciones de los Griegos de la medida indirecta de distancias y ángulos en la "esfera celestial" como así sus medidas de las tierras inundadas por el Río Nilo. La palabra "trigonometría", basada en las palabras Griegas para las medidas de triángulo, fue utilizada por primera vez como un título para un texto por el matemático alemán Pitiscus en 1600 A.C.
Originalmente, las funciones trigonométricas fueron restringidas a ángulos y sus aplicaciones a la medida indirecta de ángulos y distancias. Estas funciones gradualmente se liberaron de las restricciones, y ahora existe funciones trigonométricas de números reales. Las aplicaciones modernas varían sobre muchos tipos de problemas y tienen poco o nada que ver con ángulos o triángulos.
Funciones Trigonométricas de Ángulos.
Estas se definieron en el triángulo rectángulo para el ángulo indicado. Son conocidas como razones trigonométricas
Recuerde que un triángulo rectángulo es aquel triángulo que tiene un ángulo recto (90°). La relación entre los lados en estos triángulos es c2=a2+b2.
Matriz de clasificación de las características de las gráficas de funciones trigonométricas
CARACTERÍSTICAS DE LA GRÁFICA DE y = sen(x)
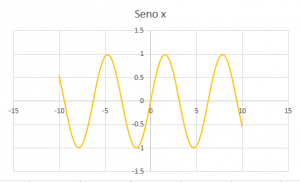
El ciclo de la función seno comienza en 0 y termina en 2π.
Dominio: el conjunto de números reales
Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
Cruza el eje de “y” en (0,0)
El eje de referencia es: eje “x”.
El punto máximo es: (π/2,1)
El punto mínimo es: (3π/2,-1)
Su período: 2π.
CARACTERÍSTICAS DE LA GRÁFICA DE y = cos(x)
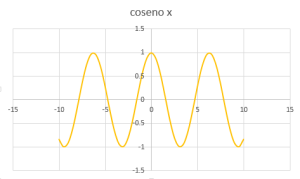
El ciclo fundamental de la función coseno del ángulo comienza en 0 y termina en 2π.
Dominio: el conjunto de números reales.
Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
Cruza el eje de “y” en: (0,1)
El eje de referencia es: el eje “x”
El punto máximo es: (0,1) y (2π,1)
El punto mínimo es: (π,-1)
Su período: 2π
CARACTERÍSTICAS DE LA GRÁFICA DE y = tan(x)
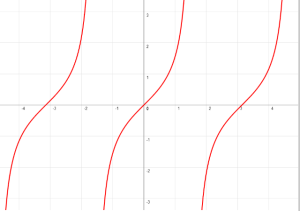
El ciclo fundamental de la función tangente del ángulo comienza en -π/2 y termina en π/2.
Tiene asíntotas en el ciclo.
Dominio: toda x diferente a (π/2)±nπ
Alcance: el conjunto de todos los números reales.
Cruza el eje de “y” en (0,0)
El eje de referencia es: el eje “x”
El punto máximo es:
El punto mínimo es:
Su período: π
Asíntotas: x=±π/2
CARACTERÍSTICAS DE LA GRÁFICA DE y = cot(x)
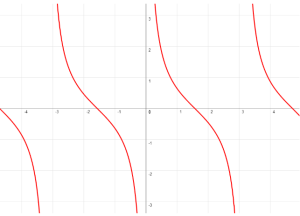
El ciclo fundamental de la función cotangente del ángulo comienza en 0 y termina en π.
Tiene asíntotas en el ciclo.
Dominio: toda x diferente a ±nπ
Alcance: el conjunto de todos los números reales.
No cruza el eje de “y”
El eje de referencia es: el eje “x”.
Su período: π
asíntotas: x=±nπ
CARACTERÍSTICAS DE LA GRÁFICA DE y = sec(x)
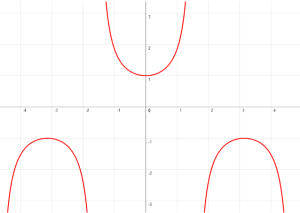
El ciclo fundamental de la función secante del ángulo comienza en -π/2 y termina en 3π/2.
Tiene tres asíntotas verticales.
Dominio: el conjunto de números reales excepto los múltiplos impares de π/2
Alcance: el conjunto de todos los números reales menores menores o iguales que –1 y todos los números mayores o iguales que 1
Cruza el eje de “y” en (0,1)
El eje de referencia es: el eje “x”
El punto máximo es: (π,-1)
El punto mínimo es: (0, 1)
Su período: 2π
Asíntotas: x=-π/2, x=π/2 y x=3π/2
CARACTERÍSTICAS DE LA GRÁFICA DE y = csc(x)
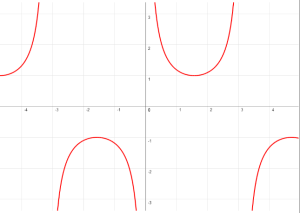
El ciclo fundamental de la función cosecante del ángulo comienza en 0 y termina en 2π.
Tiene tres asíntotas.
Dominio: el conjunto de números reales excepto los multiplos impares de π/2
Alcance: el conjunto de todos los números menores o iguales que -1 y todos los números mayores o iguales que1
Cruza el eje de “y” en (0,1)
El eje de referencia es: el eje “x”
El punto máximo es: (π,-1)
El punto mínimo es: (0, 1)
Su período: 2π
Asíntotas: x=-π/2, x=π/2 y x=3π/2
Ley de los senos y cosenos
La ley de los senos es la relación entre los lados y ángulos de triángulos no rectángulos (oblicuos). Simplemente, establece que la relación de la longitud de un lado de un triángulo al seno del ángulo opuesto a ese lado es igual para todos los lados y ángulos en un triángulo dado.
En ∆ABC es un triángulo oblicuo con lados a, b y c , entonces .
.
Ángulo de referencia
Digamos que θ es un ángulo de ningún cuadrante en posición estándar. Su ángulo de referencia es el ángulo agudo a formado por el lado terminal de θ y el eje horizontal.
Cuadrante I: El ángulo dado y el ángulo de referencia son el mismo ángulo.
α = θ

Cuadrante II: α = π – θ (radianes)
α = 180°– θ (grados)

Cuadrante III: α = θ – π (radianes)
α = θ – 180° (grados)

Cuadrante IV: α = 2 π – θ (radianes)
α = 360° – θ (grados)

Circulo unitario y funciones trigonométricas
Las funciones trigonométricas, parece haber tenido su origen en las investigaciones de los Griegos de la medida indirecta de distancias y ángulos en la "esfera celestial" como así sus medidas de las tierras inundadas por el Río Nilo. La palabra "trigonometría", basada en las palabras Griegas para las medidas de triángulo, fue utilizada por primera vez como un título para un texto por el matemático alemán Pitiscus en 1600 A.C.
Originalmente, las funciones trigonométricas fueron restringidas a ángulos y sus aplicaciones a la medida indirecta de ángulos y distancias. Estas funciones gradualmente se liberaron de las restricciones, y ahora existe funciones trigonométricas de números reales. Las aplicaciones modernas varían sobre muchos tipos de problemas y tienen poco o nada que ver con ángulos o triángulos.
Funciones Trigonométricas de Ángulos.
Estas se definieron en el triángulo rectángulo para el ángulo indicado. Son conocidas como razones trigonométricas
Recuerde que un triángulo rectángulo es aquel triángulo que tiene un ángulo recto (90°). La relación entre los lados en estos triángulos es c2=a2+b2.
Matriz de clasificación de las características de las gráficas de funciones trigonométricas
CARACTERÍSTICAS DE LA GRÁFICA DE y = sen(x)

El ciclo de la función seno comienza en 0 y termina en 2π.
Dominio: el conjunto de números reales
Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
Cruza el eje de “y” en (0,0)
El eje de referencia es: eje “x”.
El punto máximo es: (π/2,1)
El punto mínimo es: (3π/2,-1)
Su período: 2π.
CARACTERÍSTICAS DE LA GRÁFICA DE y = cos(x)

El ciclo fundamental de la función coseno del ángulo comienza en 0 y termina en 2π.
Dominio: el conjunto de números reales.
Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
Cruza el eje de “y” en: (0,1)
El eje de referencia es: el eje “x”
El punto máximo es: (0,1) y (2π,1)
El punto mínimo es: (π,-1)
Su período: 2π
CARACTERÍSTICAS DE LA GRÁFICA DE y = tan(x)

El ciclo fundamental de la función tangente del ángulo comienza en -π/2 y termina en π/2.
Tiene asíntotas en el ciclo.
Dominio: toda x diferente a (π/2)±nπ
Alcance: el conjunto de todos los números reales.
Cruza el eje de “y” en (0,0)
El eje de referencia es: el eje “x”
El punto máximo es:
El punto mínimo es:
Su período: π
Asíntotas: x=±π/2
CARACTERÍSTICAS DE LA GRÁFICA DE y = cot(x)

El ciclo fundamental de la función cotangente del ángulo comienza en 0 y termina en π.
Tiene asíntotas en el ciclo.
Dominio: toda x diferente a ±nπ
Alcance: el conjunto de todos los números reales.
No cruza el eje de “y”
El eje de referencia es: el eje “x”.
Su período: π
asíntotas: x=±nπ
CARACTERÍSTICAS DE LA GRÁFICA DE y = sec(x)

El ciclo fundamental de la función secante del ángulo comienza en -π/2 y termina en 3π/2.
Tiene tres asíntotas verticales.
Dominio: el conjunto de números reales excepto los múltiplos impares de π/2
Alcance: el conjunto de todos los números reales menores menores o iguales que –1 y todos los números mayores o iguales que 1
Cruza el eje de “y” en (0,1)
El eje de referencia es: el eje “x”
El punto máximo es: (π,-1)
El punto mínimo es: (0, 1)
Su período: 2π
Asíntotas: x=-π/2, x=π/2 y x=3π/2
CARACTERÍSTICAS DE LA GRÁFICA DE y = csc(x)

El ciclo fundamental de la función cosecante del ángulo comienza en 0 y termina en 2π.
Tiene tres asíntotas.
Dominio: el conjunto de números reales excepto los multiplos impares de π/2
Alcance: el conjunto de todos los números menores o iguales que -1 y todos los números mayores o iguales que1
Cruza el eje de “y” en (0,1)
El eje de referencia es: el eje “x”
El punto máximo es: (π,-1)
El punto mínimo es: (0, 1)
Su período: 2π
Asíntotas: x=-π/2, x=π/2 y x=3π/2
Ley de los senos y cosenos
La ley de los senos es la relación entre los lados y ángulos de triángulos no rectángulos (oblicuos). Simplemente, establece que la relación de la longitud de un lado de un triángulo al seno del ángulo opuesto a ese lado es igual para todos los lados y ángulos en un triángulo dado.
En ∆ABC es un triángulo oblicuo con lados a, b y c , entonces
 .
.
Ley de los cosenos
En todo triangulo se cumple que conociendo 2 lados y el ángulo comprendido entre ellos, se puede conocer el tercer lado
Esto supone 3 posibilidades:

EJERCICIOS DE LA PAGINA 48
Esto supone 3 posibilidades:
EJERCICIOS DE LA PAGINA 48
Un cateto cualquiera es igual a otro cateto multiplicado por la tangente del angulo opuesto al cateto buscado, o por la cotangente del angulo agudo adyacente a dicho cateto
II. USO DE LA FUNCIÓN SENO
46. Problema directo. Si en un triangulo rectángulo se conocen el angulo agudo y el cateto opuesto, o el angulo agudo y la hipotenusa, se puede calcular la hipotenusa o el cateto opuesto al angulo dado , valiéndose de la función seno
EJEMPLO 1. La hipotenusa de un triangulo rectángulo mide 16 m, y el angulo B es de 35´40´.
Calculese el cateto b
POR FORMULA t= a X sen B
se obtiene = 16 X .5830 = 9.32 m
2. El cateto b de un triangulo rectangulo tiene 23.75 m y el angulo agudo B es de 39´50´,
Cuanto mide la hipotenusa
APLICANDO LA FORMULA a= b/sen B
se obtiene = a = 23.75/.6406 =37.07 m
47. Problema inverso. Calcule el angulo agudo , dados la hipotenusa y el cateto opuesto al angulo que se busca.
EJEMPLO. Calcular el angulo B del triangulo rectangulo BAC, en el cual la hipotenusa mide 50 m y el cateto b, 34.10 m
DE LA FORMULA seno B = b/a
se deduse = seno B = 34.10 /50 =.6820
Por las tablas se obtiene = 43 grados
EJERCICIO 9
CALCULESE EL CATETO b SABIENDO QUE :
1.a=26.45 B=37´20´
2. a=54.17 B=58´45´
3. a=32.27 B=39´50´
4. a=52.56 B=37´26´
5. a=125.34 B=49´37´
6. a=324.43 B=17´38´
POR LA FORMULA t=a X sen B
RESPUESTAS
1. 16.04 m
2. 46.31 m
3. 20.67 m
4. 31.94 m
5. 95.47 m
6. 98.27 m
POR FORMULA t= a X sen B
se obtiene = 16 X .5830 = 9.32 m
2. El cateto b de un triangulo rectangulo tiene 23.75 m y el angulo agudo B es de 39´50´,
Cuanto mide la hipotenusa
APLICANDO LA FORMULA a= b/sen B
se obtiene = a = 23.75/.6406 =37.07 m
47. Problema inverso. Calcule el angulo agudo , dados la hipotenusa y el cateto opuesto al angulo que se busca.
EJEMPLO. Calcular el angulo B del triangulo rectangulo BAC, en el cual la hipotenusa mide 50 m y el cateto b, 34.10 m
DE LA FORMULA seno B = b/a
se deduse = seno B = 34.10 /50 =.6820
Por las tablas se obtiene = 43 grados
EJERCICIO 9
CALCULESE EL CATETO b SABIENDO QUE :
1.a=26.45 B=37´20´
2. a=54.17 B=58´45´
3. a=32.27 B=39´50´
4. a=52.56 B=37´26´
5. a=125.34 B=49´37´
6. a=324.43 B=17´38´
POR LA FORMULA t=a X sen B
RESPUESTAS
1. 16.04 m
2. 46.31 m
3. 20.67 m
4. 31.94 m
5. 95.47 m
6. 98.27 m
EJERCICIOS DE LA PAGINA 49
CALCULESE LA HIPOTENUSA SABIENDO QUE :
7. b= 42 B=37´40´
8. b=56.48 B=75´20´
9. b= 72.46 B=35´40´
10. b=75 B=35´43´
11. b=37.40 B=27´36´
12. b=125.54 B= 36´57´
POR LA FORMULA a= b/sen B
RESPUESTAS
7. 68.73 m
8. 58.38 m
9. 124.27 m
10. 128.47 m
11. 80.72 m
12. 208.84 m
CALCULESE EL ANGULO B, SABIENDO QUE :
13. a=37.42 b=21.20
14. a=56.81 b=17.14
15. a=24.35 b=8.93
16. a=32.44 b=65.43
17. a=12.21 b=54.12
18. a=42.34 b=45.48
POR LA FORMULA sen B = b/ a
RESPUESTAS
13.123.02 m
14.324.1 m
15.30.76 m
16. 82.0 m
17.73.11 m
18.119.54 m
19.Una escalera de 9 m. está apoyada contra un pared . ¿Qué altura alcanza si forma con el suelo , supuesto horizontal, un angulo de 72 grados?
20.Se inscribe un decagono regular en una circunferencia de 5 cm de radio. Calcula la longitus de dicho poligono.
21.¿Cual es el radio de la circunferencia cirucunscrita a un heptagono regular de 2 cm de lado?
22. Se necesita conocer la distancia norte-sur de un terreno cercado .Para esto trazan las rectas ON y OS y se mide el angulo NOS , que resulta de 38 grados , ¿ Cual es la distancia , si de N a O hay 300 m y la recta NS es perpendicular a OS?
23. Un obrero tiene una escalera de 12 m ¿Que angulo debe hacerle formar con el suelo , si quiere alcanzar una altura de 9 m? 60 grados
24.La luz de un puente forma un angulo de 66 grados , correspondiente a una cuerda de 34 m .
Calculese el radio de dicha area
25.El angulo de la base de un triangulo isosceles es de 34 grados y la altura de 15 m. Calculese la longitud de cada uno de los lados iguales
26. Supuesta la tierra esferica y el radio ecuatorial , de 6378 km, calcular la distancia BC del plano del tropico de Cáncer al plano
EJERCICIOS DE LA PAGINA 50
del ecuador , sabiendo que los trópicos están a 23´27´ del ecuador.
27. Cuanto mide , según los datos del problema anterior , el radio DC de cada uno de los trópicos, y cual es la longitud circunferencial correspondiente?
28 ¿Cuál es , en km, la longitud de un arco comprendido entre 2 puntos situados sobre el paralelo 48´50´, si la diferencia de longitudes es de 15 grados?
29. ¿Cuantos km hay que recorrer sobre el paralelo 40 grados para que el arco correspondiente sea 10 grados ?
III. USO DE LA FUNCIÓN COSENO
48. Problema directo. Si en un triangulo rectángulo se conocen un angulo agudo y el cateto adyacente , o un angulo agudo y la hipotenusa ,se puede calcular la hipotenusa o el cateto adyacente al angulo dado, por medio de la función coseno
EJEMPLO 1. El angulo B de un triangulo rectangulo es de 25 grados y el cateto adyacente c mide 34 m. Calculese la hipotenusa
DE LA FORMULA a = c/cos B
se obtine a= 34/.9063 = 37.51 m
2. La hipotenusa de un triangulo rectangulo es de 23 m y el angulo agudo B , de 47 grados. Calculese el cateto c
DE LA FORMULA c = a cos B
se deduce c= 23X68.20=15.686 m
49. Problema inverso. Calculo de un angulo agudo, dados la hipotenusa y el cateto adyacente al angulo que se busca
EJEMPLO. Hallar el valor del angulo agudo B del triangulo rectángulo BAC en el que la hipotenusa mide 20 cm y el cateto c, 7 cm
Según los dato, se tiene: cos B =c/a = 7/20= .35
Por las tablas se obtiene : 69´31´
CALCULESE LA HIPOTENUSA SABIENDO QUE :
7. b= 42 B=37´40´
8. b=56.48 B=75´20´
9. b= 72.46 B=35´40´
10. b=75 B=35´43´
11. b=37.40 B=27´36´
12. b=125.54 B= 36´57´
POR LA FORMULA a= b/sen B
RESPUESTAS
7. 68.73 m
8. 58.38 m
9. 124.27 m
10. 128.47 m
11. 80.72 m
12. 208.84 m
PAGINAS 24 Y 25 GEOMETRÍA PLANA Y TRIGONOMÉTRICA
7. LEY DE LOS SENOS Y LEY DEL COSENO
EJERCICIOS
1.Dos puestos de observación están alineados con una torre.Desde el puesto mas lejano el angulo de elevación al punto más alto de la torre es de 18 grados y desde el más cercano, situado a 20 metros del anterior, el ángulo de elevación al mismo punto de la torre es de 26 grados 30´.
Calculen la distancia del puesto de observación más lejano a la torre
La distancia es
2. Dos barcos, A y B parten de una misma estación situada en un punto R en direcciones que forman un ángulo de 73 grados 30´. El barco A lleva una velocidad de 11 km/hr mientras que el barco B lleva una velocidad de 15 km/hr.¿A que distancia se encontrarán uno del otro a los 45 minutos de viaje?
3. Un agricultor observa que su terreno tiene forma de trapecio y determina que las longitudes de los lados paralelos del trapecio son 25 metros y 34 metros.Además, mide los ángulos de la base (se asume como base el lado mayor de los paralelos) y observa que las medidas son 33 grados 20´ y 40 grados 50´.Calculen la medida de los lados no paralelos .
4. Para subir una caja desde la cuneta de una carretera hasta la cinta asfáltica se utiliza un tablón de 2.5 metros de longitud, como se muestra en la figura .El angulo que forma el piso de la cuneta con el desplante de la carretera es de 125 grados y la longitud del desplante es de 80 metros ¿A qué distancia del inicio del desplante se apoya el tablón?
5. Las longitudes de las manecillas del horario y minutero de un reloj son 12 cm y 20 cm respectivamente ¿A que distancia se encuentran sus extremos cuando son la 5 horas?
6. Un asta de bandera esta situada en la parte más alta de una montaña.Desde un punto de observación situado a nivel de la montaña, un tipógrafo midió los ángulos de elevación a los puntos más altos y más bajos del asta, que son 45 grados y 36 grados respectivamente. Calcula altura de la montaña, la asta mide 8 metros.
7.Un árbol de 6 metros de altura se encuentra en la cima de un montículo de como se muestra en la figura. Calcula la distancia de la base del montículo a la parte más alta del árbol.
8. Calcula la longitud del radio de la circunferencia circunscrita a un heptágono regular si su diagonal de menor longitud mide 42 cm
Agustín Anfonssi pagina 61, 62, 63
ejercicio 1. respuesta :22.29 grados
ejercicio 2. respuesta : 50.24
ejercicio 3 respuesta : 0.88 km
ejercicio 4 respuesta : 140 m
ejercicio 5 respuesta :11.126 m
ejercicio 6 respuesta:643.35 m
ejercicio 7 respuesta:0.64 m
ejercicio 8 respuesta: . 3915 grados
ejercicio 9 respuesta : 5.06 km
pagina de la guía 192
4.
5.
6.
7.
8.
9.
EJERCICIOS
1.Dos puestos de observación están alineados con una torre.Desde el puesto mas lejano el angulo de elevación al punto más alto de la torre es de 18 grados y desde el más cercano, situado a 20 metros del anterior, el ángulo de elevación al mismo punto de la torre es de 26 grados 30´.
Calculen la distancia del puesto de observación más lejano a la torre
La distancia es
2. Dos barcos, A y B parten de una misma estación situada en un punto R en direcciones que forman un ángulo de 73 grados 30´. El barco A lleva una velocidad de 11 km/hr mientras que el barco B lleva una velocidad de 15 km/hr.¿A que distancia se encontrarán uno del otro a los 45 minutos de viaje?
4. Para subir una caja desde la cuneta de una carretera hasta la cinta asfáltica se utiliza un tablón de 2.5 metros de longitud, como se muestra en la figura .El angulo que forma el piso de la cuneta con el desplante de la carretera es de 125 grados y la longitud del desplante es de 80 metros ¿A qué distancia del inicio del desplante se apoya el tablón?
5. Las longitudes de las manecillas del horario y minutero de un reloj son 12 cm y 20 cm respectivamente ¿A que distancia se encuentran sus extremos cuando son la 5 horas?
6. Un asta de bandera esta situada en la parte más alta de una montaña.Desde un punto de observación situado a nivel de la montaña, un tipógrafo midió los ángulos de elevación a los puntos más altos y más bajos del asta, que son 45 grados y 36 grados respectivamente. Calcula altura de la montaña, la asta mide 8 metros.
7.Un árbol de 6 metros de altura se encuentra en la cima de un montículo de como se muestra en la figura. Calcula la distancia de la base del montículo a la parte más alta del árbol.
8. Calcula la longitud del radio de la circunferencia circunscrita a un heptágono regular si su diagonal de menor longitud mide 42 cm
Agustín Anfonssi pagina 61, 62, 63
ejercicio 1. respuesta :22.29 grados
ejercicio 2. respuesta : 50.24
ejercicio 3 respuesta : 0.88 km
ejercicio 4 respuesta : 140 m
ejercicio 5 respuesta :11.126 m
ejercicio 6 respuesta:643.35 m
ejercicio 7 respuesta:0.64 m
ejercicio 8 respuesta: . 3915 grados
ejercicio 9 respuesta : 5.06 km
pagina de la guía 192
4.
5.
6.
7.
CONSTRUYE T
1.6 LIDIAR CON LAS DIFICULTADES
Actividad 1
a. Lean la siguiente historia
Habia una ves un hombre llamado Santiago. En la pedregosa tierra donde vivían todos caminaban descalzos.Un día, cansado de las espinas y de las piedras que lo lastimaban, quiso encontrar un medio para proteger sus pies. Así que se le ocurrió una solución: cubrir todos lo caminos con pieles de vaca."La ruta sera suave, esas espinas no podrán lacerarme", pensó. Entusiasmado, fue a compartir el plan con su abuela"abuela"le dijo, "tengo un gran ideal y, así se la contó"
La vieja le contesto con ternura"¿donde podría encontrase suficiente cuero para cubrir la superficie de la tierra ? ¿No seria mas fácil cortar dos pedazos de cuero para hacerte unos zapatos?. Así sería como si todo el mundo estuviese cubierto con piel".
b. Ahora imaginemos las espinas y las piedras de la la historia como a nuestra compañera Yeni y al hecho de que no se anima a preguntar en la clase de matemáticas:
¿Cual seria una estrategia basada en"cubrir los caminos con pieles de vaca"? pues cambiarse de casa o escuela, cambiar los temas de matemáticas o no verlos y no hablarle a su papa
¿Cuales serian "ponerse los zapatos"? pues tratar de cambiar su situación emocional ante sus adversidades o su actitud ante esos problemas
Actividad 2. Piensa en otra espina (dificultad) recurrente de la clase de matemáticas y completen aquí o en su cuaderno
Actividad 1
a. Lean la siguiente historia
Habia una ves un hombre llamado Santiago. En la pedregosa tierra donde vivían todos caminaban descalzos.Un día, cansado de las espinas y de las piedras que lo lastimaban, quiso encontrar un medio para proteger sus pies. Así que se le ocurrió una solución: cubrir todos lo caminos con pieles de vaca."La ruta sera suave, esas espinas no podrán lacerarme", pensó. Entusiasmado, fue a compartir el plan con su abuela"abuela"le dijo, "tengo un gran ideal y, así se la contó"
La vieja le contesto con ternura"¿donde podría encontrase suficiente cuero para cubrir la superficie de la tierra ? ¿No seria mas fácil cortar dos pedazos de cuero para hacerte unos zapatos?. Así sería como si todo el mundo estuviese cubierto con piel".
b. Ahora imaginemos las espinas y las piedras de la la historia como a nuestra compañera Yeni y al hecho de que no se anima a preguntar en la clase de matemáticas:
¿Cual seria una estrategia basada en"cubrir los caminos con pieles de vaca"? pues cambiarse de casa o escuela, cambiar los temas de matemáticas o no verlos y no hablarle a su papa
¿Cuales serian "ponerse los zapatos"? pues tratar de cambiar su situación emocional ante sus adversidades o su actitud ante esos problemas
Actividad 2. Piensa en otra espina (dificultad) recurrente de la clase de matemáticas y completen aquí o en su cuaderno
ESPINA: Tener que hacer los trabajos que no entiendo ya que son muy difíciles o complejos
ESTRATEGIA"CUBRIR LOS CAMINOS CON PIELES": Estudiar toda mi vida matemáticas dejando atrás todos mis sueños para que todos los problemas se me hagan fáciles
ESTRATEGIA "PONERSE ZAPATOS": Este ese tema bien para no volverme a atrasar o estresar por no entenderlo y acabarlo para volver con mis actividades que me gustan
Actividad 3. En plenaria comenten ¿Qué diferencia hay en ambas estrategias? que una es mil veces mas fácil que otra y menos tardada
¿Qué beneficios te traería si eliges la estrategia de ponerte zapatos para lidiar con tus dificultades?
pues te ahorras muchísimo tiempo y es mas rápido
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA LECCIÓN: Qué pues siempre hay que pensar en una manera efectiva y cómoda para estas situaciones y pensar mejor las cosas
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA LECCIÓN: Qué pues siempre hay que pensar en una manera efectiva y cómoda para estas situaciones y pensar mejor las cosas
2.6 QUITARNOS LAS ETIQUETAS QUE NO NOS AYUDAD
Actividad 1:trabajen de manera individual. Carlos hizo su mapa de etiquetas .Uso algunas etiquetas que él considera que lo definen.Otras etiquetas se relacionan con lo que otros dicen de él.
Las etiquetas que lo ayudan a lograr sus metas y a estar bien están en rojo y las etiquetas que no lo ayudan en azul.
Realiza tu mapas de etiquetas
3.6 REGULAR LAS EMOCIONES ENTRENANDO LA MENTE
Actividad 1. Trabajen en equipos de 3 o 4 estudiantes.Observen la foto de Naty en la clase de matemáticas.
a.¿Qué le pudo haber pasado? pues haber tenido todas las respuestas mal en su examen
b.¿Qué emoción imaginan que siente? nervios, miedo y enojo
c. Anoten el recuerdo diferentes pensamiento que se imaginan que podría tener Naty
Actividad 1. Trabajen en equipos de 3 o 4 estudiantes.Observen la foto de Naty en la clase de matemáticas.
a.¿Qué le pudo haber pasado? pues haber tenido todas las respuestas mal en su examen
b.¿Qué emoción imaginan que siente? nervios, miedo y enojo
c. Anoten el recuerdo diferentes pensamiento que se imaginan que podría tener Naty
"dios, no puedo se que me pasara esto" "mi papa, que va a decir mi papa" "por favor, que alguien me ayude" "Odio esto, enserio lo odio"
Actividad 2. Tomen el primer pensamiento de Naty que anotaron
a.¿Es realista o exagerada esta valoración? realista
Justifica tu respuesta dando dos argumentos que la sustenten:pues que simplemente esta pensando como le puede pasar eso a ella, como a cualquier persona normal y que prácticamente es lo primero que piensa uno cuando le llega a pasar algo de ese estilo
Actividad 2. Tomen el primer pensamiento de Naty que anotaron
a.¿Es realista o exagerada esta valoración? realista
Justifica tu respuesta dando dos argumentos que la sustenten:pues que simplemente esta pensando como le puede pasar eso a ella, como a cualquier persona normal y que prácticamente es lo primero que piensa uno cuando le llega a pasar algo de ese estilo
b.¿Qué le dirían a Naty para ayudarla con base en la reflexión de los incisos anteriores ? "oye ¿estas bien?" "así pasa, ya veras que luego todo pasara"
c. ¿Cómo podría sentirse mejor?Expliquen su respuesta?
Pues sencillamente apoyándola , haciéndola sentir que tiene apoyo de alguien
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA LECCIÓN
Que aunque haya malos momentos, pasaran, por que después de la tormenta llega la calma , todo pasara y mejoraras como persona
4.6 EL BOTÓN DE LA ANSIEDAD ACADÉMICA
Actividad 1
a. De manera individual , lee los siguientes comentarios:
NIÑA:¿Que situación me causa malestar? pues ,definitivamente hacer los ejercicios de matemáticas yo sola, me siento mal cuando no me salen a la primera
NIÑO: a mi me pasa cuando tengo que hablar en la clase de ingles , tiemblo mucho , se me olvidan las palabras
NIÑO: siento lo mismo cuando paso al lado del grupito que va en el ultimo año , me dan miedo y siento que me podrían molestar
b. Describe una situación que te cause malestar,nerviosismo, rechazo, etcétera . Escribe que pensabas en ese momento y qué sentías en tu cuerpo.:pues una vez que tenia que hacer una mascara de un personaje, no sabia como rayos iba a hacer una mascara, ni como decorarla, estaba super confundido
c. La situación del inciso anterior probablemente sea de ansiedad académica . revisa la definición del concepto clave y responde¿Qué implicación ha tenido la ansiedad académica en tu vida escolar? pues gracias a ella tengo mucho o tenia mucho nerviosismo ante cualquier tarea importante, grande o larga
¿Qué consecuencias te podría traer a futuro? darme miedo al querer una carrera muy difícil y exigente que me guste
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA REACCIÓN
Qué aunque sea mala la ansiedad académica, se puede vencer si te esfuerzas en ello
5.6 TRABAJAR EL BOTÓN DE LA ANSIEDAD
Actividad 1. Trabajen en completando el ultimo cuadro de la historia que te presentamos a continuación
Primer examen de matemáticas: deje el estudio para el ultimo momento, no me dio tiempo de cubrir todos los temas y me acosté tarde. Dormí mal. No alcance a desayunar, llegue corriendo , tarde y con agitación. Sentía incomodidad y mis músculos estaban tensos, me empece a sentir mal, no podia concentrarme en el examen.Este conflicto interno entre quererme sentir mejor y tener que aprobar el examen fue muy desagradable. Así paso 2 veces .
MARIANA MARTINEZ
MI BOTÓN: Presentar exámenes de matemáticas
EMOCIÓN QUE ME GENERA:Ansiedad
ESTRATEGIA PARA CAMBIAR ESE BOTÓN (MUNDO O SITUACIÓN): Para el próximo examen de matemáticas voy a estudiar con tiempo y poco a poco
TERCER EXAMEN: Estudie con tiempo, cubrí estudiar todos los temas y me acosté temprano para el examen, dormí bien, desayune tranquilo, llegue tranquilo al salón, con tiempo, estaba relajada, me sense y me sentí normal, empece a concentrarme en el examen y al final me fue de maravilla
Actividad 2 en la variación 4.6 que escribiste de una situación recurrente ("botón")
a. Anótala nuevamente : una vez que tenia que hacer una mascara de un personaje , no sabia como rayos iba a hacer una mascara ni como decorarla, estaba confundido
b. piensa y anota cómo podrías aplicar la "estrategia de cambiar al mundo para disminuir su intensidad": pensar con la mente tranquila y fría , pensando rápido que usare para decorar esa mascara y sobretodo como hacerla
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA LECCIÓN: que siempre si quiere estar tranquilo sin preocupaciones , has lo que tengas que hacer con tiempo
6.6 CUANDO LLEGA EL HURACAN
a. Lean el siguiente texto
Alejandria y Paconio eran dos pueblos vecinos a los que se les aviso de la venida de un huracan, Alejandria se preparo, reforzo sus casas, guardaron agua, comida , linternas y velas, mientras paconio dijo que no habia problema con el huracan que seria suave.El huracan llego, fue muy fuerte y dejo sin luz ni agua en varios dias, muchas casas se levantaron.
a. Ahora imaginemos a dos estudiantes: maria y omar , ambos les llega el botón del enojo cuando deben hacer equipos de matemáticas, maria se calma y se prepara pero omar ocupa la estrategia de paconio
b. completen la siguiente
1.¿Qué hace antes de que llegue el enojo? 2.¿Qué hace, piensa durante el enojo? 3.¿qué hace después?
OMAR 1.empieza a enojarse antes de unirse al grupo 2. no coopera con el grupo y sigue enojado 3.se relaja todavía con el enojo que sigue teniendo
MARIA 1.se empieza a relajar para no estresarse 2.se auto controla y trabaja con el grupo 3. se relaja y lo olvida
MARIA 1.se empieza a relajar para no estresarse 2.se auto controla y trabaja con el grupo 3. se relaja y lo olvida
Actividad 3 contesta de manera individual
a.Anota una emoción que hayas sentido en alguna clase donde hayas actuado como los habitantes de paconio
cuando yo tenia planeado un viaje por un gran tiempo y la semana todo el tiempo estuvo libre de tareas, pero justo el viernes todos atacaron con tareas y yo la verdad me enoje tanto que la deje
b. ¿consideras que estabas distraído?explica por que
no, solo lo ignore, si hubiera estado distraído ni siquiera me habría enterado de la tarea
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA LECCIÓN
Qué en toda situación siempre podrás elegir la postura que tomas, la buena o la mala, la que tu prefieras, la de paconio y alejandria pero hasta responsable ya que traen sus consecuencias las 2
ESCRIBE EN UN MINUTO QUE TE LLEVAS DE LA LECCIÓN
Qué en toda situación siempre podrás elegir la postura que tomas, la buena o la mala, la que tu prefieras, la de paconio y alejandria pero hasta responsable ya que traen sus consecuencias las 2















No hay comentarios.:
Publicar un comentario